Фокус с матрицей

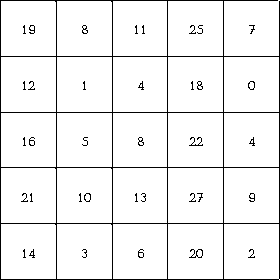
Приготовьте пять монет и 20 бумажных фишек. Попросите кого-нибудь выбрать любое из чисел, вписанных в клетки квадрата (см. рисунок). Положите на это число монету и закройте все остальные числа, стоящие в одной строке и одном ряду с выбранным, фишками.

Попросите теперь того же человека выбрать любое из чисел, вписанных в незакрытые еще клетки, положите на выбранное число другую монету, а числа, стоящие в той же строке и в том же столбце, что и выбранное во второй раз число, снова закройте фишками.

Повторите эту процедуру еще два раза, вы обнаружите, что незакрытой осталась лишь одна клетка. Положите на эту клетку пятую монету.

Если теперь вычислить сумму чисел, накрытых монетами (напомним, что на первый взгляд числа кажутся выбранными наудачу), то она будет равна 57. Это не случайно: сколько бы вы ни повторяли эксперимент, сумма всегда будет одной и той же.

Секрет фокуса: квадрат представляет собой не что иное, как самую обычную таблицу сложения, правда, составленную весьма замысловатым образом. Строится такая таблица с помощью двух наборов чисел: 12, 1, 4, 18, 0 и 7, 0, 4, 9, 2. Сумма всех этих чисел равна 57. Написав числа первого набора над верхней строкой квадрата, а числа второго набора слева от самого левого столбца, вы сразу же поймете, как получаются числа в клетках квадрата.

Так, число в левом верхнем углу (стоящее на пересечении первой строки и первого столбца) равно сумме чисел 12 и 7. Точно также получаются и все остальные числа: для того чтобы узнать, какое число следует вписать в ту или иную клетку, нужно просто вычислить сумму чисел, стоящих у той строки и того столбца, на пересечении которых находится интересующая нас клетка.

Совершенно аналогичным образом можно построить магический квадрат любого размера с любыми числами. Сколько клеток в квадрате и какие числа выбраны для его построения, никакой роли не играет.

Числа в исходных наборах могут быть положительными или отрицательными, целыми или дробными, рациональными или иррациональными. Получившаяся таблица всегда будет обладать волшебным свойством: проделав описанную выше процедуру с монетами и фишками, вы всегда получите сумму чисел, входящих в оба исходных набора. В частности, в рассмотренном нами случае можно было взять любые восемь чисел, дающих в сумме 57.

Теперь уже нетрудно понять основную идею фокуса. Число, стоящее в любой клетке квадрата, равно сумме каких-то двух чисел в исходных наборах. Положив монету на выбранное число, вы тем самым как бы вычеркиваете эти два числа. Каждая новая монета кладется на пересечение другой строки с другим столбцом, поэтому пяти монетам соответствует сумма пяти пар выбранных нами исходных чисел, которая, разумеется, равна сумме всех десяти исходных чисел.

Один из наиболее простых способов построить таблицу сложения с помощью квадратной матрицы заключается в следующем. Впишем в левый верхний угол 1 и будем продолжать нумерацию клеток слева направо последовательными целыми положительными числами. Заполненную матрицу 4х4 можно рассматривать как таблицу сложения для двух наборов чисел: 1, 2, 3, 4 и 0, 4, 8, 12. Сумма чисел, оказавшихся под монетками, в такой матрице всегда будет равна 34.

Получающаяся сумма, разумеется, зависит от размеров квадрата. Если число клеток, умещающихся вдоль стороны квадрата, обозначить через n, то сумма будет равна (n3+n)/2.

Квадраты с нечетным n дают сумму, равную произведению n и числа, стоящего в центральной клетке. Если нумерацию клеток начать с числа a, большего 1, и продолжать по порядку, то сумма окажется равной ((n3+n)/2)*n(a-1).

Интересно заметить, что точно такой же будет сумма чисел в любом столбце и в любой строке традиционного магического квадрата, составленного из тех же числовых элементов.

С помощью второй формулы легко найти, каким должно быть число в левом верхнем углу матрицы любых размеров, чтобы она давала наперед заданную сумму. Огромное впечатление производит следующий фокус, который можно показать экспромтом. Попросив кого-нибудь назвать любое число, больше 30 (это позволит избежать отрицательных чисел), вы тут же чертите матрицу 4х4, которая будет давать сумму, равную только что указанному числу! (Для быстроты, вместо того чтобы закрывать числа монетками, можно обводить их кружочками, а строки и столбцы, на пересечении которых стоят выбранные числа, вычеркивать.)

Чтобы продемонстрировать этот фокус, вам придется проделать единственную выкладку (ее нетрудно произвести в уме): вычесть 30 из названного числа, а разность разделить на 4. Пусть, например, названо число 43. Вычитая 30, вы получаете 13. Разделив его на 4, находите число 31/4. Вписав 31/4 в левый верхний угол матрицы 4х4 и продолжив далее по порядку 41/4, 51/4 и т.д., вы получите магический квадрат с суммой, равной 43.

Чтобы еще больше запутать зрителя, числа в квадрате следует переставить. Например, первое число 31/4 можно вписать в клетку, стоящую в третьей строке, а три следующих числа (41/4, 51/4 и 61/4) расположить в той же строке, но в произвольном порядке.

Следующие четыре числа можно расположить в любой строке, но в том же порядке, в каком вы вписывали первые четыре числа. То же самое нужно проделать и с двумя оставшимися четверками чисел.

Если вы не желаете иметь дело с дробными числами, но по-прежнему хотите получить сумму, равную 43, то дробь 1/4 у всех чисел можно отбросить, а к числам, стоящим в верхней строке, прибавить по единице (в результате чего в верхней строке окажутся числа 16, 17, 18 и 19). Точно так же, если бы дробная часть первого числа бала равна 2/4, к числам, стоящим в верхней строке, нужно было бы прибавлять 2, а если бы дробная часть оказалась равной 3/4 - 3.

Перестановка строк и столбцов не меняет магических свойств квадрата, но делает матрицу более загадочной, чем она есть на самом деле.

Фокус можно показывать и с таблицей умножения. В этом случае выбранные числа нужно не складывать, а умножать. Полученное произведение всегда равно произведению чисел, с помощью которых построена таблица.